Chapter 22 Linear Predictors and Inverse Link Functions

The fun brickr package converts images into a mosaic made of Lego building blocks. The above mosaic is put here to emphasize that we are learning building blocks for making models of data-generating processes. Each block is used to make some mathematical representation of the real-world. The better our representations, the better our insights. Instead of using Lego bricks, our tool of choice is the generative DAG. We have almost all the building blocks we need, latent nodes, observed nodes, calculated nodes, edges, plates, linear models, and probability distributions, but this chapter introduces one last powerful building block - the inverse link function.
The range of a function is the set of values that the
function can give as output. For a linear predictor with non-zero slope,
this range is any number from -
22.1 Linear Predictors
This chapter, we focus on restricting the range of linear predictors. A linear predictor for data observation,
where
Explanatory variable effects are fully summarized in the corresponding coefficients,
22.2 Inverse Link Functions
An inverse link function takes linear predictor output, which ranges from -
- Exponential: The exponential function converts a linear predictor of the form
- Inverse Logit (aka logistic): This function provides a way to convert a linear predictor of the form
While the beauty of these functions is that it allows us to use the easily-understood linear model form and still also have a form that is useful in a generative DAG. The downside is we lose interpretability of the coefficients. The only thing we get to say easily is that higher values of the linear predictor correspond to higher values of the transformed output.
When communicating the effects of explanatory variables that are put through inverse link functions, you should either: 1) simulate observed data using the prior or posterior’s generative recipe, or 2) consult one of the more rigorous texts on Bayesian data analysis for some mathematical tricks to interpreting generative recipes with these inverse link functions (see references at end of book).
22.2.1 Exponential Function
Figure 22.1 takes a generic example of a Poisson count variable and makes the expected rate of occurrence a function of an explanatory variable.
For a specific example, think about modelling daily traffic ticket in New York City. The expected rate of issuance would be a linear predictor based on explanatory variables such as inches of snow, holiday, president in town, end-of-month, etc. Since linear predictors can turn negative and the rate parameter of a Poisson random variable must be strictly positive, we use the exponential function to get from linear predictor to rate.
library(causact)
dag_create() %>%
dag_node("Count Data","k",
rhs = poisson(rate),
obs = TRUE) %>%
dag_node("Exp Rate","rate",
rhs = exp(y),
child = "k") %>%
dag_node("Linear Predictor","y",
rhs = alpha + beta * x,
child = "rate") %>%
dag_node("Intercept","alpha",
child = "y") %>%
dag_node("Explantory Var Coeff","beta",
child = "y") %>%
dag_node("Observed Expl Var","x",
child = "y",
obs = TRUE) %>%
dag_plate("Observation","i",
nodeLabels = c("k","rate","y","x")) %>%
dag_render()Figure 22.1: A generative DAG that converts a linear predictor into a strictly positive number.
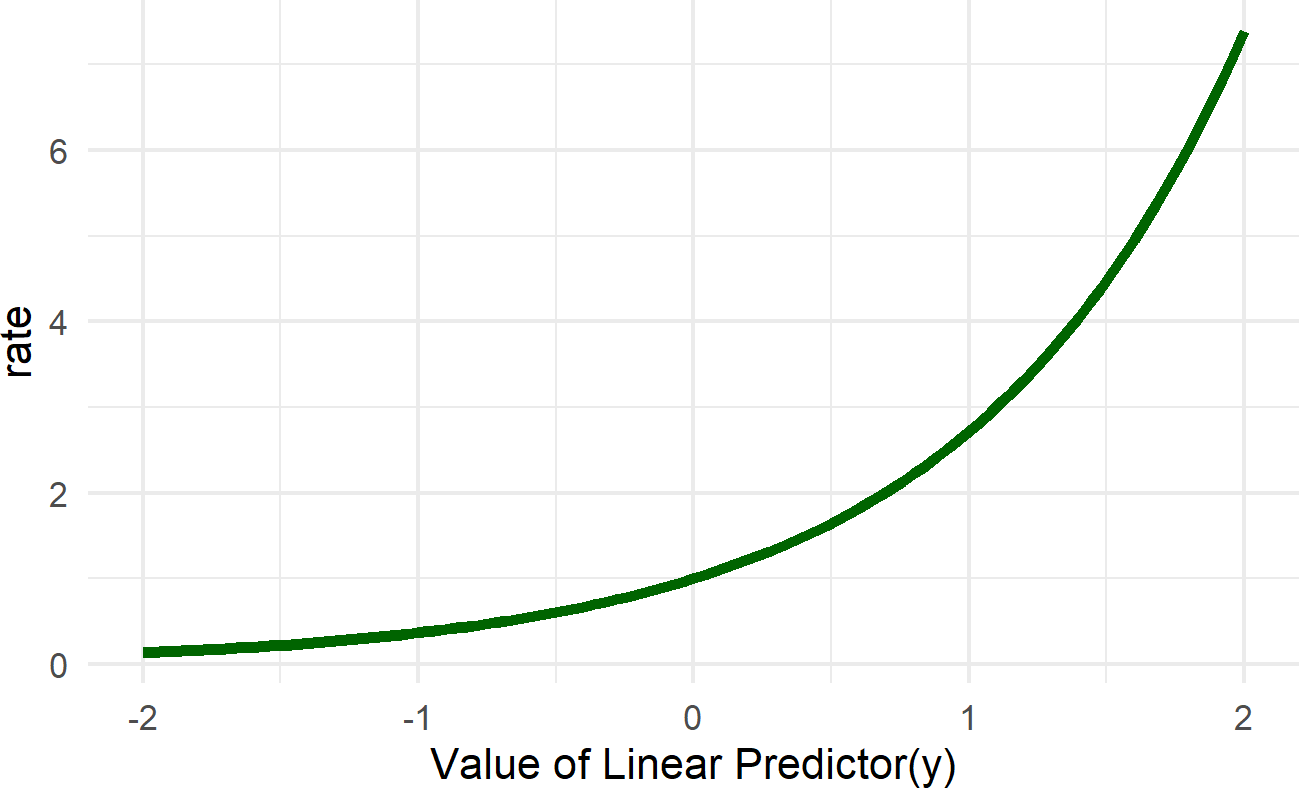 Figure 22.2: Graph of the exponential function. The linear predictor in our case is alpha + beta * x. The role of the exp function is to map this linear predictor to a scale that is non-negative. This essentailly takes any number from -infinity to infinty and provides a positive number as an output.
Figure 22.2: Graph of the exponential function. The linear predictor in our case is alpha + beta * x. The role of the exp function is to map this linear predictor to a scale that is non-negative. This essentailly takes any number from -infinity to infinty and provides a positive number as an output.
The inverse link function transformation takes place in the node for rate. The linear predictor,
From Figure 22.2, we see that negative values of the linear predictor are transformed into values of rate between 0 and 1 and positive values of the linear predictor get transformed into rate values greater than 1. Notice this transformation is non-linear, and hence caution must be used interpreting the slope coefficients of the linear predictor. We will see this in the next chapter.
22.2.2 Inverse Logit
Figure 22.3 shows a generic generative DAG which leverages the inverse logit link function.
library(causact)
dag_create() %>%
dag_node("Bernoulli Data","z",
rhs = bernoulli(theta),
obs = TRUE) %>%
dag_node("Success Probability","theta",
rhs = 1 / (1+exp(-y)),
child = "z") %>%
dag_node("Linear Predictor","y",
rhs = alpha + beta * x,
child = "theta") %>%
dag_node("Intercept","alpha",
child = "y") %>%
dag_node("Explantory Var Coeff","beta",
child = "y") %>%
dag_node("Observed Expl Var","x",
child = "y",
obs = TRUE) %>%
dag_plate("Observation","i",
nodeLabels = c("z","theta","y","x")) %>%
dag_render()Figure 22.3: A generative DAG that converts a linear predictor into a value between 0 and 1.
The use of the inverse logit function is done inside a method called logistic regression. Check out this sequence of videos that begin here (https://youtu.be/zAULhNrnuL4) on logistic regression for some additional insight.
Note the inverse link function transformation takes place in the node for theta. To start to get a feel for what this transformation does, observe Figure 22.4. When the linear predictor is zero, the associated probability is 50%. Increasing the linear predictor will increase the associated probability, but with diminishing effect. When the linear predictor is increased by one unit from say 1 to 2, the corresponding probability goes from about 73% to 88% (i.e. from
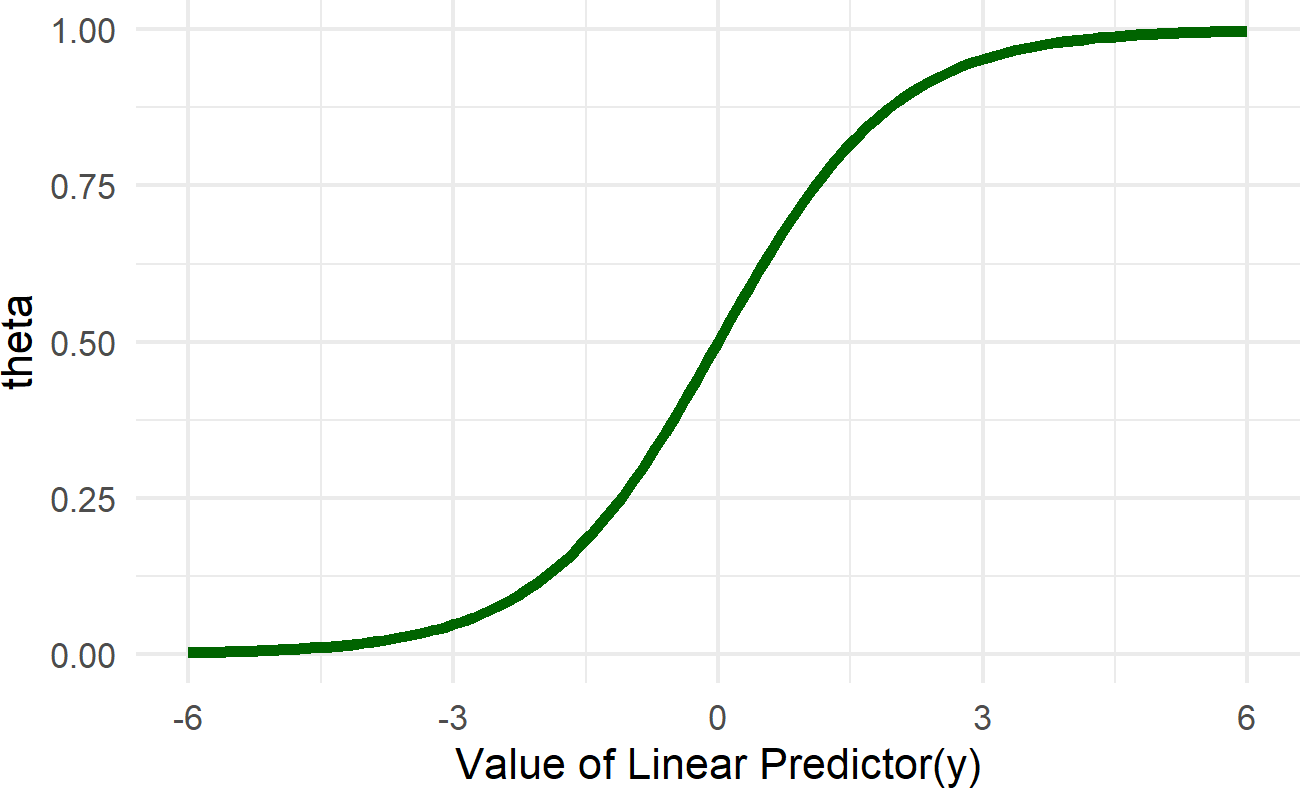 Figure 22.4: Graph of the inverse logit function (aka the logistic function). The linear predictor in our case is alpha + beta * x. The role of the inverse logit function is to map this linear predictor to a scale bounded by zero and one. This essentailly takes any number from -infinity to infinty and provides a probability value as an output.
Figure 22.4: Graph of the inverse logit function (aka the logistic function). The linear predictor in our case is alpha + beta * x. The role of the inverse logit function is to map this linear predictor to a scale bounded by zero and one. This essentailly takes any number from -infinity to infinty and provides a probability value as an output.
Almost anytime you are modelling a probability as a function of many explanatory variables, using the inverse logit-link function is an obvious choice to make the mathematics work.
22.3 Building Block Training Complete
You have officially been exposed to all the building blocks you need for executing Bayesian inference of ever-increasing complexity. These include latent nodes, observed nodes, calculated nodes, edges, plates, probability distributions, linear predictors, and inverse-link functions. While you have not seen every probability distribution or every inverse-link function, you have now seen enough that you should be able to digest new instances of these things. In the next chapter, we seek to build confidence by increasing the complexity of the business narrative and the resulting generative DAG to yield insights. Insights you might not even have thought possible!
22.4 Exercises
Exercise 22.1 Assume a linear predictor,
Exercise 22.2 Continue from the previous exercise with the following additional information. According to your data analysis, a certain process change lowers the value of the linear predictor by 0.4 to
Exercise 22.3 Assume a linear predictor,